‘The usual suspects’: Euler diagrams of letter signatories as a practical application for set theory

The day before the 2017 Labour Party Conference in Brighton, Labour Vision published an essay in which I argued that responsible non-Jews on the Left should take note of majority Jewish opinion, and not ignore it in favour of tiny minority groups on the fringes of the Jewish community whose opinion happens to be more convenient for Leftists. What actually happened at the conference is history — and quite unpleasant history at that (for details, I recommend reading both Marcus Dysch’s overview of events and David Collier’s eyewitness account). There’s much more to be said on the topic, and I’ll get around to saying some of it before long, but for now, I’d like to revisit the odd little centrepiece of my Labour Vision essay: the analysis of signatories to four letters opposing action against antisemitism. (tl;dr: There are very few Jews who are committed anti-Zionists, but the anti-Zionist movement needs them in order to maintain the impression of not being anti-Jewish, so a lot of the same names get recycled between different open letters to the press. Also, a tutorial on how to make Euler diagrams in R. Something for everyone?)

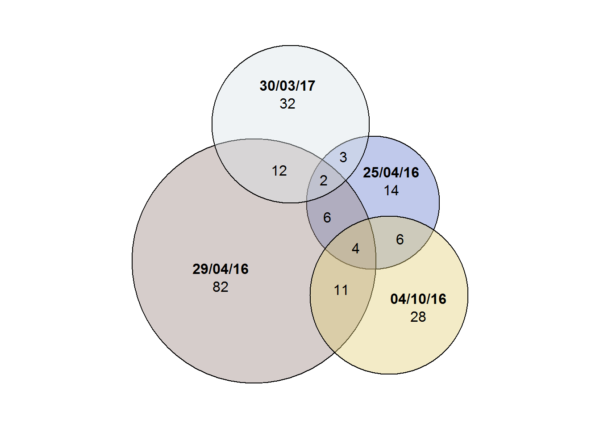
The above is an Euler diagram, which is like a Venn diagram except in that its role is to show actual overlaps rather than hypothetical ones. Each of the four circles represents the signatories to an open letter. Overlaps between circles show where the same people signed multiple letters, and these are labelled to show how great the overlaps were. (Not all overlaps were possible to represent using circles, which is something we’ll come to below.) The letters are as follows:

• the Guardian letter of 29 April 2016 insisting that the ‘tiny number of cases of real antisemitism’ in the Labour Party are only a distraction from the ‘much more widespread examples of Islamophobia and xenophobia in the Conservative and other parties’ (signatories identified as ‘Jewish members and supporters of the Labour party and of Jeremy Corbyn’s leadership’)
• the Guardian letter of 4 October 2016 rejecting the EU Monitoring Centre on Racism’s working definition on antisemitism and insisting that ‘[t]he decision of Momentum’s steering committee and its chair Jon Lansman to remove Jackie Walker as vice-chair [for reasons related to alleged antisemitism] is a betrayal of the trust of thousands of Momentum members’ (signatories identified as ‘Jewish members and supporters of Momentum’)
• the letter published on Ken Livingstone’s website on 30 March 2017 complaining of ‘a skilfully delivered campaign to present the Left of the Labour Party as riddled with antisemitism’ (signatories identified as ‘Jewish members and supporters of the Labour Party’)
• the letter published by the Independent on 25 April 2016 stating that ‘Israel is no longer believed when denying responsibility for its crimes against Palestinians, so now its supporters resort to silencing opposition to those crimes with blanket allegations of anti-Semitism’ (signatories identified as ‘mainly Jewish’)

Why these four letters? Because they were all recent, because they all had the same purpose, i.e. the rubbishing of allegations of antisemitism on the Left, and because they all identified their signatories as ‘Jewish’ or ‘mainly Jewish’.

The purpose of accumulating multiple signatories for a letter is not what Aristotle called logos, or appeal to reason, but ethos, or appeal to the credibility of the speaker — which in this case means of those in whose name the letter is sent. What is it that makes these signatories so credible as to be worth adding to the letter? In telling us that all or most of their signatories write in their capacity as Jews, the letters instruct us to take them credibly for their Jewishness.

How might this help the letters to achieve their purpose? The risk in saying that accusations of Jew-hate are a Jewish lie is that one may be taken for a Jew-hater in one’s own right — and therefore as an unreliable witness in matters of Jew-hating. But the risk of being taken for a Jew-hater will always be less if one is able to position oneself as a Jew.

It’s not that those who wish to say the sorts of things that antisemites say but don’t wish to be taken for antisemites are short of options. For example, those who are not Jewish can introduce themselves as people ‘of Jewish ancestry’, or — failing that — can insist that there are a great many Jews who would agree with whatever it is that they are saying if only they were here right now. The latter is what I call the ‘imaginary Jewish friends’ approach. But, for rhetorical effectiveness, nothing beats ‘as a Jew’.

Many of the same signatures have also appeared on letters that had the same purpose but that did not identify their signatories in religious or ethnic terms. These were ignored because they weren’t making the same claim of ethos. Then there was the letter that identified its signatories — again including many shared names — as ‘Jewish and non-Jewish’. It was ignored because its bid for ethos was so clearly doomed: if you want to give the impression that your position is widespread among Jews, but you need non-Jews to make up the numbers, then something has gone terribly wrong.¹

More than once, I have heard Jews respond to such lists of Jewish signatories with a sniff: ‘The usual suspects.’ And certainly, the same names seem to crop up over and over again. Their importance to the Left appears to be very great. David Collier puts it thus:

The central way that… institutions fend off criticism of their ideological opposition to mainstream Jewry is through the use of the Jewish 5%. The anti-Zionist Jews. Every community has a 5%. With Jews, this tiny minority, normally of Marxist or near-Marxist leaning, are ideologically opposed to Zionism. The remnants of movements like the Bundists, who were annihilated in the Holocaust. Many of these are on the fringes of the community, and their identification as a Jewish anti-Zionist is the only Jewish identification that still exists in their lives.

‘Not just one Jew, but many Jews hereby affirm that accusations of Jew-hate are unfounded, and therefore those accusations must be unfounded indeed’ is the sub-text of all four letters. But that begs the question, ‘How many Jews?’ Collier’s ‘5%’ (though probably not intended as an estimate of actual numbers) suggests that it can’t be very many. ‘The usual suspects’ suggests that it’s the same Jews, over and over again.

To investigate this phenomenon, we can make very simple use of an area of mathematics called set theory. A set is a collection of entities, however defined. In this case, the entities are people who have signed letters. The union of two sets, A and B, encompasses every entity that is in set A or in set B: for example, all the people who have signed either of two letters. The intersection of two sets, A and B, encompasses every entity that is in set A and in set B: for example, all the people who have signed both of two letters.

Let’s say we have two letters with ten signatures each. If ten people signed one letter and ten different people signed the other, then the union of the sets of signatories will be twenty and the intersection will be zero. On the other hand, if it is the same ten people signing both letters, then the union will be ten and the intersection will also be ten, because the two apparent sets will be in reality a single set. Studying sets of signatories in this way enables us to see how much recycling of signatories has to be done between letters in order to create the impression of persuasive ethos. Euler diagrams — which were developed as a way of representing relationships between sets — provide the most obvious way of visualising the findings.

So here’s the methodology:

1. For each of the four letters above, collect the signatures and treat them as a set of entities
2. Calculate the intersections between all possible combinations of the four resulting sets
3. Represent those intersections using an Euler diagram

The letters were all available online, so step 1 was easy: a copy-and-paste job (correcting spelling errors and removing titles as I went). From that point onwards, I did all the work in R. To get going, I stored the signatures for each of the four letters in a separate vector. Unlike Python, R doesn’t have a specific data structure with which to represent sets. However, it can carry out set operations — such as calculating unions and intersections — on vectors. When it does this, it treats all the unique elements of each vector as a set and ignores repetitions.

This is how to get the intersection of two sets of signatories, represented as vectors named a and b:

intersect(a, b)
## [1] "Tony Greenstein" "Richard Kuper" "Leah Levane" 
## [4] "Rachel Lever"    "Helen Marks"   "Jonathan Rosenhead"

That’s the actual intersection (i.e. the names of the people who signed both letters — at least two of which you are likely to have seen before if you have seen letters like this). Now to get the size of the intersection:

length(intersect(a, b))
## [1] 6

Six it is! Getting the intersection of three is a little trickier (the third is called c; no prizes for guessing the name of the fourth):

# Using vanilla R:

length(intersect(intersect(a, b), c))
## [1] 4

# Doing the same thing, but using the 'pipe' (i.e. the %>% symbol between commands) from the dplyr package instead of nested parentheses (recommended for readability):

library(dplyr)

a %>% intersect(b) %>% intersect(c) %>% length
## [1] 4

So of the six signatories in both a and b, just two were not also in c. Here’s how to get the size of the union of all four, i.e. the total number of people who signed one or more of the letters:

a %>% union(b) %>% union(c) %>% union(d) %>% length
## [1] 120

And here, for comparison, is the sum of the numbers of signatures that each letter has (i.e. allowing double-, triple-, and quadruple-counting of names that appeared in multiple letters):

c(a, b, c, d) %>% length
## [1] 156

156 signatures, but only 120 signatories.

To visualise the intersections with an Euler diagram, I used the eulerr R package. A particularly nice feature of this package is that it makes the area of each circle — and each overlap — as closely proportional as possible to the size of the set or intersection in question. It doesn’t, however, calculate those sizes for us: instead, the user has to tell it how big all the sets and intersections are by passing it a named vector of numbers. The numbers in the vector are the counts of entities in the various sets and intersections between sets. The names given to the numbers let the euler function know which sets or intersections the counts pertain to. You can give a set any sensible name. To indicate an intersection, give the names of the sets in question, separated by ampersand symbols. I know that sounds confusing, so I’ll start by demonstrating the general principle.

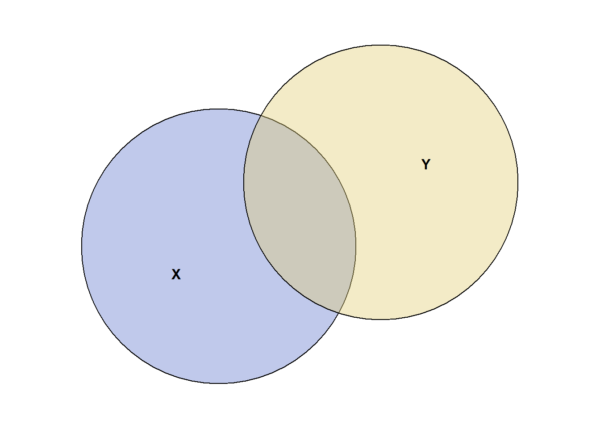
Here’s a simple example, where X and Y are sets with three members each, of which one is shared between both:

library(eulerr)

overlaps <- c('X' = 3,
              'Y' = 3,
              'X&Y' = 1)

fit <- euler(overlaps)

plot(fit)

It would be a pain in the neck to work out all the overlaps by hand and copy them out into a bit of code like the above, so instead we’ll include the calculations in the definition of the vector. Here’s a silly example. Everything is the same, except that instead of numbers, we’re entering code to calculate numbers:

mammals <- c('horse', 'kangaroo', 'giant pangolin')
exclusive.quadrupeds <- c('horse', 'crocodile', 'diplodocus')

overlaps <- c('X' = length(mammals),
              'Y' = length(exclusive.quadrupeds),
              'X&Y' = intersect(mammals, exclusive.quadrupeds) %>% length)

fit <- euler(overlaps)

plot(fit)

Same result. (The rotation is random.)

Now for the real thing (this time also instructing R to provide counts showing the size of each set and intersection, as well as meaningful labels):

overlaps <- c('A' = length(a),
              'B' = length(b),
              'C' = length(c),
              'D' = length(d),
              'A&B' = intersect(a, b) %>% length,
              'B&C' = intersect(b, c) %>% length,
              'C&D' = intersect(c, d) %>% length,
              'D&A' = intersect(d, a) %>% length,
              'A&C' = intersect(a, c) %>% length,
              'D&B' = intersect(d, b) %>% length,
              'A&B&C' = a %>% intersect(b) %>%
                intersect(c) %>% 
                  length,
              'B&C&D' = b %>% intersect(c) %>%
                intersect(d) %>% 
                  length,
              'C&D&A' = c %>% intersect(d) %>%
                intersect(a) %>% 
                  length,
              'A&C&D' = a %>% intersect(c) %>%
                intersect(d) %>% 
                  length,
              'A&B&D' = a %>% intersect(b) %>%
                intersect(d) %>% 
                  length,
              'A&B&C&D' = a %>% intersect(b) %>%
                intersect(c) %>% 
                  intersect(d) %>% 
                    length)

fit <- euler(overlaps)

plot(fit, labels = c('25/04/16', '29/04/16', '04/10/16', '30/03/17'), counts = TRUE)

And there we have it: the code to generate the diagram at the top of this page. Not bad! With increasing numbers of sets of signatories (or sets of any other kind of entity), Euler diagrams quickly cease to be practical or readable, but with four, they work pretty well. Looking at a diagram like the one above, anyone can see at a glance that there are overlaps between the groups of signatories, and — through labelling and approximately proportional areas — also see how great the overlaps are.

One problem: you can’t represent all the intersections that exist between the four sets using approximately proportional overlaps between circles. It’s just not geometrically possible, so some of them get left out. One person signed all four, and six people signed two letters whose circles couldn’t be made to overlap, but you can’t deduce either of these facts from the above diagram. This means that the recycling of signatures is actually understated by this approach to visualisation. To overcome that problem, we’d need to give up on circles and use some other shape instead, but the eulerr package can’t do that currently. We could also give up on Euler diagrams and use something else: I’ve used matrices and social network graphs to visualise intersections between larger numbers of sets, for example, but they’re much harder to read and — in any case — they can only show intersections between pairs of sets.

In sum: intersections and unions of sets provide a powerful tool for studying signatories to open letters, and Euler diagrams are a visually effective way of showing that the perception of ‘the usual suspects’ at work is founded in observed reality, even if they can’t show the full extent of the phenomenon.

Oh, and — before we forget — let’s see an end to the argument that, because some members of a particular community say that X isn’t prejudiced against that community, any accusations of prejudice against it on the part of X must be lies. Because that’s a non sequitur. Diagrams or no.

Looking at you, Paul Flynn.